关于坐标旋转方法介绍:
关键词:空间旋转、旋转轴 用途:相机位姿估计、无人机位姿估计、3D游戏、3D建模 文章类型:概念、公式总结(本文不带推导过程,若想了解公式是如何推出来的请搜索文献),C++函数展示
@Date:2016-11-04 @Lab: CvLab202@CSU 写在前面的一些概念右手系关于这个概念,搞3D的人应该都懂,而像我这样做图像处理的可能就对这个知道的比较少了。右手系这个概念其实很简单,看图就懂了。在坐标系中,右手摆成下图的样子,当拇指指向X轴食指指向Y轴时,中指指向了Z轴,满足这个条件的坐标系就是右手系。本文所有概念都在右手系下进行讨论。 右手系
旋转90°到底是怎么转当我要让一个点,绕Y轴转动了90°,并且用程序计算出了旋转结果,为了验证这个点是否旋转正确,我们需要知道这个90°是怎么转的。在网上搜索了挺多文章,都没有对这个东西进行明确的定义,那么这里给出我的总结。从原点(0,0,0)往Y轴方向看,此时视野中的坐标系降维到二维坐标系XOZ,那么让点绕O点顺时针转90°,即为正确的旋转结果。
问题一:XYZ空间内某点绕X、Y、Z轴旋转一次这个问题比较简单,网上已经有较多总结: 设旋转前坐标为 ,旋转后坐标为 ,旋转后坐标为 。 。 1.绕Z轴旋转γ角首先给出向量表示: <span id="MathJax-Element-1-Frame" class="mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="[x′,y′,z′,1]=[x,y,z,1][cosγsinγ00−sinγcosγ0000100001]" role="presentation" style="padding-top: 1px; padding-bottom: 1px; display: inline-block; line-height: 0; font-size: 21.96px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">[x′,y′,z′,1]=[x,y,z,1]⎡⎢⎢⎢⎢⎣cosγsinγ00−sinγcosγ0000100001⎤⎥⎥⎥⎥⎦[𝑥′,𝑦′,𝑧′,1]=[𝑥,𝑦,𝑧,1][cos𝛾sin𝛾00−sin𝛾cos𝛾0000100001] 然后是公式表示: <span id="MathJax-Element-2-Frame" class="mjx-full-width mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="(1)x′=cosγ⋅x−sinγ⋅y(2)y′=sinγ⋅x+coγ⋅y(3)z′=z" role="presentation" style="padding-top: 1px; padding-bottom: 1px; line-height: 0; font-size: 21.96px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 9.758em; min-height: 0px; border: 0px; width: 10000em; position: relative; display: table-cell !important;">x′=cosγ⋅x−sinγ⋅yy′=sinγ⋅x+coγ⋅yz′=z(1)(2)(3)(1)𝑥′=𝑐𝑜𝑠𝛾⋅𝑥−𝑠𝑖𝑛𝛾⋅𝑦(2)𝑦′=sin𝛾⋅𝑥+𝑐𝑜𝛾⋅𝑦(3)𝑧′=𝑧 最后是代码表示
- <table width="98%" class="t_table"><tbody><tr><td>//将空间点绕Z轴旋转
- //输入参数 x y为空间点原始x y坐标
- //thetaz为空间点绕Z轴旋转多少度,角度制范围在-180到180
- //outx outy为旋转后的结果坐标
- void codeRotateByZ(double x, double y, double thetaz, double& outx, double& outy)
- {
- double x1 = x;//将变量拷贝一次,保证&x == &outx这种情况下也能计算正确
- double y1 = y;
- double rz = thetaz * CV_PI / 180;
- outx = cos(rz) * x1 - sin(rz) * y1;
- outy = sin(rz) * x1 + cos(rz) * y1;
- }
- </td></tr></tbody></table>
[/table]
2.绕Y轴旋转β角首先给出向量表示: <span id="MathJax-Element-3-Frame" class="mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="[x′,y′,z′,1]=[x,y,z,1][cosβ0−sinβ00100sinβ0cosβ00001]" role="presentation" style="padding-top: 1px; padding-bottom: 1px; display: inline-block; line-height: 0; font-size: 21.96px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">[x′,y′,z′,1]=[x,y,z,1]⎡⎢⎢⎢⎣cosβ0−sinβ00100sinβ0cosβ00001⎤⎥⎥⎥⎦[𝑥′,𝑦′,𝑧′,1]=[𝑥,𝑦,𝑧,1][cos𝛽0−sin𝛽00100sin𝛽0cos𝛽00001] 然后是公式表示: <span id="MathJax-Element-4-Frame" class="mjx-full-width mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="(4)x′=cosβ⋅x+sinβ⋅z(5)y′=y(6)z′=−sinβ⋅x+cosβ⋅z" role="presentation" style="padding-top: 1px; padding-bottom: 1px; line-height: 0; font-size: 21.96px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 10.78em; min-height: 0px; border: 0px; width: 10000em; position: relative; display: table-cell !important;">x′=cosβ⋅x+sinβ⋅zy′=yz′=−sinβ⋅x+cosβ⋅z(4)(5)(6)(4)𝑥′=𝑐𝑜𝑠𝛽⋅𝑥+𝑠𝑖𝑛𝛽⋅𝑧(5)𝑦′=𝑦(6)𝑧′=−sin𝛽⋅𝑥+cos𝛽⋅𝑧 最后是代码表示
- <table width="98%" class="t_table"><tbody><tr><td>//将空间点绕Y轴旋转
- //输入参数 x z为空间点原始x z坐标
- //thetay为空间点绕Y轴旋转多少度,角度制范围在-180到180
- //outx outz为旋转后的结果坐标
- void codeRotateByY(double x, double z, double thetay, double& outx, double& outz)
- {
- double x1 = x;
- double z1 = z;
- double ry = thetay * CV_PI / 180;
- outx = cos(ry) * x1 + sin(ry) * z1;
- outz = cos(ry) * z1 - sin(ry) * x1;
- }</td></tr></tbody></table>
[table=98%,none]
3.绕X轴旋转α角首先给出向量表示: <span id="MathJax-Element-5-Frame" class="mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="[x′,y′,z′,1]=[x,y,z,1][10000cosαsinα00−sinαcosα00001]" role="presentation" style="padding-top: 1px; padding-bottom: 1px; display: inline-block; line-height: 0; font-size: 21.96px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; position: relative;">[x′,y′,z′,1]=[x,y,z,1]⎡⎢⎢⎢⎣10000cosαsinα00−sinαcosα00001⎤⎥⎥⎥⎦[𝑥′,𝑦′,𝑧′,1]=[𝑥,𝑦,𝑧,1][10000cos𝛼sin𝛼00−sin𝛼cos𝛼00001] 然后是公式表示: <span id="MathJax-Element-6-Frame" class="mjx-full-width mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="(7)x′=x(8)y′=cosα⋅y−sinα⋅z(9)z′=sinα⋅y+sinα⋅z" role="presentation" style="padding-top: 1px; padding-bottom: 1px; line-height: 0; font-size: 21.96px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 9.922em; min-height: 0px; border: 0px; width: 10000em; position: relative; display: table-cell !important;">x′=xy′=cosα⋅y−sinα⋅zz′=sinα⋅y+sinα⋅z(7)(8)(9)(7)𝑥′=𝑥(8)𝑦′=cos𝛼⋅𝑦−sin𝛼⋅𝑧(9)𝑧′=sin𝛼⋅𝑦+sin𝛼⋅𝑧 最后是代码表示
- //将空间点绕X轴旋转
- //输入参数 y z为空间点原始y z坐标
- //thetax为空间点绕X轴旋转多少度,角度制范围在-180到180
- //outy outz为旋转后的结果坐标
- void codeRotateByX(double y, double z, double thetax, double& outy, double& outz)
- {
- double y1 = y;//将变量拷贝一次,保证&y == &y这种情况下也能计算正确
- double z1 = z;
- double rx = thetax * CV_PI / 180;
- outy = cos(rx) * y1 - sin(rx) * z1;
- outz = cos(rx) * z1 + sin(rx) * y1;
- }
|
问题二:空间点绕任意轴旋转首先,需要定义"任意轴"的单位向量,例如X轴可以用向量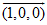 来表示。 来表示。 那么假设旋转轴的单位向量为 ,旋转前坐标为 ,旋转前坐标为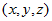 ,旋转后坐标为 ,旋转后坐标为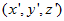 ,旋转角为 ,旋转角为 ,于是有: ,于是有: <span id="MathJax-Element-7-Frame" class="mjx-full-width mjx-chtml MathJax_CHTML" tabindex="0" data-mathml="(10)x′=(vx⋅vx⋅(1−cosθ)+cosθ)⋅x+(vx⋅vy⋅(1−cosθ)−vz⋅sinθ)⋅y+(vx⋅vz⋅(1−cosθ)+vy⋅sinθ)⋅z(11)y′=(vx⋅vy⋅(1−cosθ)+vz⋅sinθ)⋅x+(vy⋅vy⋅(1−cosθ)+cosθ)⋅y+(vy⋅vz⋅(1−cosθ)−vx⋅sinθ)⋅z(12)z′=(vx⋅vz⋅(1−cosθ)−vy⋅sinθ)⋅x+(vy⋅vz⋅(1−cosθ)+vx⋅sinθ)⋅y+(vz⋅vz⋅(1−cosθ)+cosθ)⋅z" role="presentation" style="padding-top: 1px; padding-bottom: 1px; line-height: 0; font-size: 13.4667px; overflow-wrap: normal; word-spacing: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 47.023em; min-height: 0px; border: 0px; width: 10000em; position: relative; display: table-cell !important;">x′=(vx⋅vx⋅(1−cosθ)+cosθ)⋅x+(vx⋅vy⋅(1−cosθ)−vz⋅sinθ)⋅y+(vx⋅vz⋅(1−cosθ)+vy⋅sinθ)⋅zy′=(vx⋅vy⋅(1−cosθ)+vz⋅sinθ)⋅x+(vy⋅vy⋅(1−cosθ)+cosθ)⋅y+(vy⋅vz⋅(1−cosθ)−vx⋅sinθ)⋅zz′=(vx⋅vz⋅(1−cosθ)−vy⋅sinθ)⋅x+(vy⋅vz⋅(1−cosθ)+vx⋅sinθ)⋅y+(vz⋅vz⋅(1−cosθ)+cosθ)⋅z(10)(11)(12)(10)𝑥′=(𝑣𝑥⋅𝑣𝑥⋅(1−𝑐𝑜𝑠𝜃)+𝑐𝑜𝑠𝜃)⋅𝑥+(𝑣𝑥⋅𝑣𝑦⋅(1−𝑐𝑜𝑠𝜃)−𝑣𝑧⋅𝑠𝑖𝑛𝜃)⋅𝑦+(𝑣𝑥⋅𝑣𝑧⋅(1−𝑐𝑜𝑠𝜃)+𝑣𝑦⋅𝑠𝑖𝑛𝜃)⋅𝑧(11)𝑦′=(𝑣𝑥⋅𝑣𝑦⋅(1−𝑐𝑜𝑠𝜃)+𝑣𝑧⋅𝑠𝑖𝑛𝜃)⋅𝑥+(𝑣𝑦⋅𝑣𝑦⋅(1−𝑐𝑜𝑠𝜃)+𝑐𝑜𝑠𝜃)⋅𝑦+(𝑣𝑦⋅𝑣𝑧⋅(1−𝑐𝑜𝑠𝜃)−𝑣𝑥⋅𝑠𝑖𝑛𝜃)⋅𝑧(12)𝑧′=(𝑣𝑥⋅𝑣𝑧⋅(1−cos𝜃)−𝑣𝑦⋅sin𝜃)⋅𝑥+(𝑣𝑦⋅𝑣𝑧⋅(1−cos𝜃)+𝑣𝑥⋅sin𝜃)⋅𝑦+(𝑣𝑧⋅𝑣𝑧⋅(1−cos𝜃)+cos𝜃)⋅𝑧 计算时照着公式代入即可。 最后给出代码实现:
- //定义返回结构体
- struct Point3f
- {
- Point3f(double _x, double _y, double _z)
- {
- x = _x;
- y = _y;
- z = _z;
- }
- double x;
- double y;
- double z;
- };
- //点绕任意向量旋转,右手系
- //输入参数old_x,old_y,old_z为旋转前空间点的坐标
- //vx,vy,vz为旋转轴向量
- //theta为旋转角度角度制,范围在-180到180
- //返回值为旋转后坐标点
- Point3f RotateByVector(double old_x, double old_y, double old_z, double vx, double vy, double vz, double theta)
- {
- double r = theta * CV_PI / 180;
- double c = cos(r);
- double s = sin(r);
- double new_x = (vx*vx*(1 - c) + c) * old_x + (vx*vy*(1 - c) - vz*s) * old_y + (vx*vz*(1 - c) + vy*s) * old_z;
- double new_y = (vy*vx*(1 - c) + vz*s) * old_x + (vy*vy*(1 - c) + c) * old_y + (vy*vz*(1 - c) - vx*s) * old_z;
- double new_z = (vx*vz*(1 - c) - vy*s) * old_x + (vy*vz*(1 - c) + vx*s) * old_y + (vz*vz*(1 - c) + c) * old_z;
- return Point3f(new_x, new_y, new_z);
- }
|
问题三:空间点绕xyz轴连续旋转前面的问题比较基础,到这个问题就需要一点空间想象力了。 首先我假设一个点绕x、y、z轴旋转90°,最终它会落在哪里?这个答案不是唯一的,因为旋转的顺序将会影响到最终的结果。
以点(1,2,3)为例 A 我让它首先绕x轴转90°,再绕y轴转90°,再绕z轴转90°。
- <table width="98%" class="t_table"><tbody><tr><td>double x = 1, y = 2, z = 3;
- codeRotateByX(y, z, 90, y, z);
- codeRotateByY(x, z, -90, x, z);
- codeRotateByZ(x, y, -90, x, y);
- cout << endl << " (1,2,3) -> (" << x << ',' << y << ',' << z << ")" << endl << endl;</td></tr></tbody></table>
旋转结果是: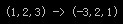
B 这一次我让它首先绕z轴转90°,再绕y轴转90°,最后绕z轴转90°。
- <table width="98%" class="t_table"><tbody><tr><td>double x = 1, y = 2, z = 3;
- codeRotateByZ(x, y, -90, x, y);
- codeRotateByY(x, z, -90, x, z);
- codeRotateByX(y, z, 90, y, z);
- cout << endl << " (1,2,3) -> (" << x << ',' << y << ',' << z << ")" << endl << endl;</td></tr></tbody></table>
这次的结果是:
显然,不同的旋转顺序导致了结果的不同,因此在处理空间内绕轴旋转的问题时,我们需要严格定义每次旋转的顺序,否则会导致错误的答案。
|